Un escalenoedro es una pirámide doble compuesta por 4 o 6 triángulos de lados desiguales, tiene 4 o 6 aristas polares más pronunciadas y 4 o 6 aristas polares menos pronunciadas que se intercambian lateral y superiormente. 

Las aristas de la parte central ascienden y descienden.   Aunque está definida como una pirámide de cuatro o seis triángulos podemos formar poliedros piramidales generados con triángulos escalenos, que son aquellos triángulos que tienen los lados distintos, y por tanto podemos categorizar esos poliedros centro de esta  clasificación.

En la figura vemos una forma de generarla, a la izquierda observamos un prisma que puede ser de sección cuadrada o rectangular y un eje de revolución que es la diagonal principal que pasa por vértices opuestos, al hacer un giro del prisma y dejar registro de 5 prismas obtenemos  el poliedro compuesto de 5 figuras que aparece en el centro de la imagen, la intersección de estos cinco prismas provoca a la derecha el escalenoedro.

Volvemos a coger el prisma de la izquierda y el eje  como diagonal principal repitiendo el mismo proceso de generación del escalenoedro a partir de la intersección en la agrupación de los cinco prismas, tenemos la figura que aparece en planta y alzado en el borde superior de la imagen, con el número 5, debajo observamos varias perspectivas del poliedro compuesto y del escalenoedro.

A la derecha volvemos a tomar el mismo prisma y el mismo eje de revolución pero ahora dejamos el registro de 6 prismas obteniendo en la intersección una dipirámide o bipirámide que es una figura formada por dos pirámides unidas por la base. En la parte inferior observamos también varias perspectivas de ambas figuras.

En la figura de la izquierda podemos observar en planta y alzado un escalenoedro con sus caras a color y con las aristas visibles y las ocultas.  A la derecha en la parte superior se ha hecho una ampliación de la franja central en la que se puede ver la intersección de los triángulos.

En la parte inferior derecha observamos otra vez la misma imagen pero hemos trazado un rectángulo por los vértices de manera que observamos la alineación.  Como podemos comprobar los vértices de los triángulos están en dos franjas, la que corresponde al lado superior del rectángulo y la que corresponde al lado inferior.

En el número 1 observamos un deltoedro que es un poliedro formado por deltoides ( trapezoides con un eje de simetría). 

En el número 2 hemos cortado el deltoedro por dos planos paralelos que pasan por vértices de los deltoides. Al separar la pieza después de haber hecho los dos cortes obtenemos tres nuevas piezas que aparecen en el número 3,  estas tres piezas son en las esquinas dos pirámides de base pentagonal regular y un antiprisma como forma central, el antiprisma está formado por 2 pentágonos cuyos planos son paralelos y por triángulos isósceles laterales.

En el número 4 observamos el antiprisma y sus dos proyecciones en planta y alzado, al haber hecho el giro del pentágono sobre el otro obtenemos en el contorno de la planta un decágono regular y su alineación de los vértices, esos puntos los subimos al alzado a su altura correspondiente.

En el caso del escalenoedro es distinto, la simetría de los triángulos escalenos provoca un decágono en color naranja y otro decágono paralelo a este a distinta altura generando también en su franja lateral triángulos por regla general escalenos. Si nos fijamos en el decágono de color naranja realmente no es un polígono regular sino que están agrupados los lados de 2 a 2 formando entre ellos ángulos distintos.

En la figura número 1 observamos el escalenoedro con los dos cortes por planos paralelos que provocan esa forma central en el medio de las dos pirámides separadas, en la figura número 2 observamos el escalenoedro en perspectiva axonométrica, en el 3 observamos el fragmento central que se obtiene después de practicar dos cortes, es un decágono con triángulos escalenos en la franja central, en esta figura se observan también las líneas ocultas mientras que en el número 4 observamos la planta y alzado del fragmento cortado pero sin incorporar las líneas ocultas.

Como podemos observar en la imagen  no siempre resulta un escalenoedro a partir de la intersección de los prismas obtenidos  en una matriz por medio del giro a 360°, podemos observar a la derecha una figura formada por caras pentagonales adyacentes a otras triangulares, una figura no catalogada hasta ahora.

Otro ejemplo distinto también a partir de un prisma de base rectangular y con la diagonal principal obtenemos mediante el giro el agrupamiento de los prismas cuya intersección provoca una figura algo irregular compuesta por triángulos y pentágonos irregulares.  Observamos a la derecha las 2 vistas en diédrico del poliedro compuesto y la intersección de los 3 prismas.

En este caso tenemos nuevamente el prisma de sección cuadrada. Al practicar el giro y registro de 5 prismas obtenemos un  deltoedro a la derecha.  Como podemos observar es una figura formada por deltoides que son trapezoides con un eje de simetría.

Al hacer la misma transformación respecto a un prisma más largo obtenemos un deltoedro más alargado,  tal y como se ve a la derecha.  Es usual que el conjunto de prismas que giran en torno a un eje provoque un deltoedro cuando dejamos registro de un número impar de prismas,  mientras que cuando el número es par suele salir un una dipirámide.

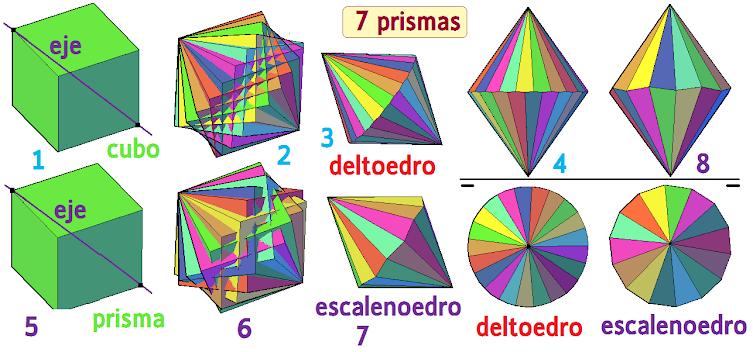
Hemos tomado en el número 1 un cubo con su diagonal principal respecto al que lo giramos y dejamos registro de cinco cubos en el número 2, en el número 3 obtenemos la intersección que es un deltoedro, figura formada por deltoides.  En el número 4 aparece la planta y alzado del deltoedro.

En el número 5 alargamos un poco el cubo y lo convertimos en un prisma, a nacer el mismo proceso de giro y dejar registro de 5 prismas obtenemos el poliedro compuesto irregular del número 6, en el 7 obtenemos la intersección que es un escalenoedro, mientras que en el 8 tenemos la planta y alzado de esta última figura.  Como podemos observar la diferencia en la anchura del prisma puede suponer como producto un deltoedro o un escalenoedro.

Hacemos el mismo proceso con 7 prismas y obtenemos nuevamente para el cubo el deltoedro (números 1, 2, 3, 4), mientras que para el prisma obtenemos el escalenoedro, (números 5 6 7 y 8).

Repetimos el mismo proceso pero ahora con 4 cubos y con 4 prismas, en el caso del cubo tras el giro del mismo y dejar registro de las cuatro figuras en el poliedro compuesto del número 6, calculamos la intersección obteniendo en el 7 una bipirámide, en el número 8 tenemos la planta y alzado de esa figura compuesta por dos pirámides unidas por la base.

En el número 1 tenemos el prisma del que hacemos el giro obteniendo el poliedro compuesto de 4 prismas, con una constitución más irregular que el del número 6 para el cubo.

En el número 3 tenemos la intersección del poliedro compuesto, como podemos ver las pirámides se deforman de manera que provocan triángulos alternos  y adyacentes de mayor y menor tamaño. 

Tenemos a la izquierda una bipirámide construida por los procedimientos anteriores, mediante el giro de un prisma en torno a su diagonal principal dejando de registro de 6 prismas, como ya vimos por regla general el número par provocaba una bipirámide o figura compuesta por dos pirámides, de la que tenemos varias proyecciones a la izquierda.

En el caso  de la derecha tenemos tres prismas cuyo registro producen en la intersección un escalenoedro.  Podemos observar que a partir de los 3 prismas entrelazados se genera el poliedro compuesto de escalenos. 

De forma general podemos decir que el número impar de prismas provoca o escalenoedros  o deltaedros,  mientras que el número par provoca bipirámides.